Since every 10 X 10 Latin square has an embedded 3 X 3 Latin square, could we seed three rows, three columns, and their intersections as the 3 X 3 Latin square?
Could your algorithm be modified to start with this additional information?

Since every 10 X 10 Latin square has an embedded 3 X 3 Latin square, could we seed three rows, three columns, and their intersections as the 3 X 3 Latin square?
Could your algorithm be modified to start with this additional information?

Could you elaborate more about this? It is unclear where exactly these 3x3 squares should be placed.

I thought about possibility to reuse existing squares and found another promising approach. You should start with existing ODLS pair of rank 8. Take first square from pair and extend it to rank 10 by appending rows and columns around this square. Then permute rows 2-9 of new square in the same way as in 2nd square from pair. You can also swap first and last rows. This looks like a promising way to find rank 10 ODLS pair.

Here is example how to turn rank 3 square into rank 5:

           O O O O O
A A A      O A A A O
B B B  =>  O B B B O
C C C      O C C C O
           O O O O O

Square after applying row permutation from 2nd square:

O O O O O
O C C C O
O B B B O
O A A A O
O O O O O

---

Since every 10 X 10 Latin square has an embedded 3 X 3 Latin square, could we seed three rows, three columns, and their intersections as the 3 X 3 Latin square?
Could your algorithm be modified to start with this additional information?

Now, used the next scheme of cells filling: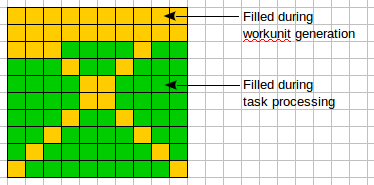

If I understand right, you ask about the next scheme: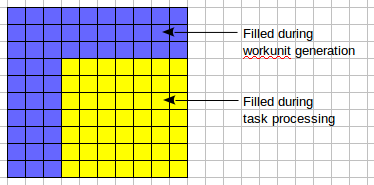

Algorithm of search can be adjusted for a scheme like showed on the second image. An idea like "get a combination of ODLS of rank n and build a combination (pair, triple, e.t.c.) of rank n+1", as I know, tested previously (not in RakeSearch) but the result was disappointing. A simple example: we know pairs of orthogonal Latin squares of rank 5. But does not exists any pair of Latin squares of rank 6. But many other schemes of building orthogonal pairs of Latin squares (diagonal and usual) exists and tested for example, in Gerasim@Home project.

Copy of this message by request of Michael:

---

As tell previously, we add some explanations about the new run of R10 search. We expect that "permutational pairs" of rank 10 - are very rare or do not even exist. In this case, 99.999% (or even 100%) results from computers contain information about a number of processed squares only. Not interesting and can hide potential errors in the algorithm. In a new application for the current run, we add to results files not the only number of processed squares and orthogonal pairs (if they are found), but partial orthogonal pairs also.
Sample of similar pair from the result, processed on my computer: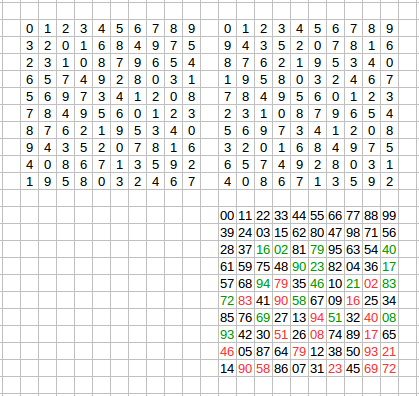

Top left square - a diagonal Latin square created during sequential generation. Top right square - generated from the first square by rows permutation. Bottom square with a two-digit number in each cell - Graeco-Latin square - the combination of two bottom squares, which were superimposed on each other. If top squares are orthogonal, all 100 two-digit numbers from Graeco-Latin square was distinct. But in this case, it is not. Only 64 values inside cells - unique (they marks by black), and other 17 numbers - present in this square more than once. If we count of distinct numbers in the bottom square we will get 81 - this is the degree of orthogonality of top pair of squares!
In the new run, we place in results all pairs with a degree of orthogonality > 80. And now, in each confirmed result we see a several or even tens partially orthogonal pairs - sometimes more than 30, for example. May be each result contain interesting information. Not ODLS, but interesting also.

---

2n X 2n Latin squares are problematic when n is odd, i.e., 6 X 6 does not exist, 10 X 10 was big news when it was found to contain a 3 X 3 --- it made the cover of Scientific American.
Unfortunately, I don't have the knowledge to contribute more. Good luck.

2n X 2n Latin squares are problematic when n is odd, i.e., 6 X 6 does not exist, 10 X 10 was big news when it was found to contain a 3 X 3 --- it made the cover of Scientific American.
Unfortunately, I don't have the knowledge to contribute more. Good luck.

Rudy, thank you! But what is your idea?

You show it in message 1118, second panel.
It looks to be asymmetric, which might be the problem with 2n X 2n squares when n is odd.
Maybe you could move to 11 X 11, if the search space is reasonable. And do 10 X 10 as Beta.

I found this paper: https://www.whitman.edu/Documents/Academics/Mathematics/2016/Horner.pdf pp 21-22, that may help.

I found this paper: https://www.whitman.edu/Documents/Academics/Mathematics/2016/Horner.pdf pp 21-22, that may help.

Thank you for link!

Hi folks!

Some interesting, (maybe fun), news, related to project scientific background. Earlier we mentioned the fill pattern. Now there is a reason to consider it in more detail: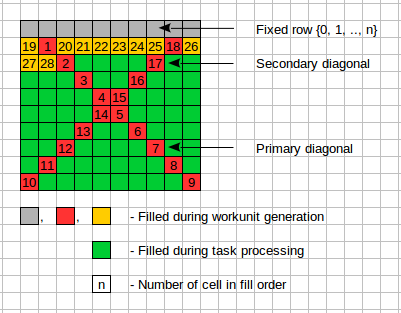

If we take the numbered cells and write out a number of combinations of filling them, we get an intrigue sequence - raise globally, but not for all cells and with different raising rates:

Cell #	Combinations
1	8
2	57
3	356
4	1909
5	8544
6	30637
7	82508
8	148329
9	133496
10	934472
11	5356527
12	26980186
13	117013695
14	424874652
15	1210593966
16	2603495520
17	3755155200
18	2723433984
19	17021462400
20	82230388428
21	341712006852
22	1187460703344
23	3329849282564
24	7024312609228
25	9908083279232
26	7996577754080
27	43965973715660
28	212963246290200

The number of combinations of first ~18 cells can be computed quickly - in several minutes. But the next steps need an hour, days and even weeks. For example for calculation of combinations for cell # 28 took ~50 days of CPU Time! This number is interesting for another reason also - it is the number of workunits for RakeSearch R10, if we try to cover an entire search space! 212963246290200 workunits! Of course, we perform a search over a small portion of the search space.

And, the second news! As you remember, every month there are many pairs with a degree of orthogonality 81, 82, ... 86. Rarely - pairs with degree 87 and 88. And no pairs with degree 89 found yet. But pair with a degree 90 found! You see it on a figure below: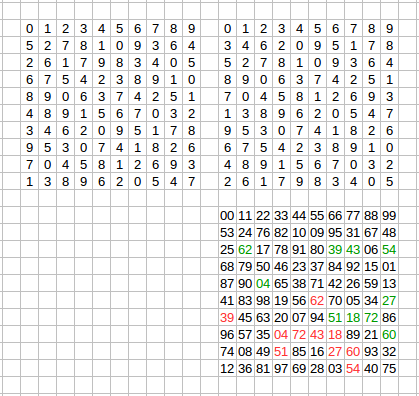


Two well-known friends of our project found this pair - josef j from Russia Team and Thyler Durden@P3D from team Planet 3DNow!.

But, of course, computations of each participant paved the way to this finding! Thank you!

What is degree of orthogonality?

What is degree of orthogonality?

Hello! We explained it in this message. In other words - degree of orthogonality of two Latin squares - is number of first occurrences of pairs in Graeco-Latin square that was build from them.

Sometimes nature has fun. When we were talking about the results of the first half of October, we noticed, that one pair with the degree of orthogonality 90 found, but no pairs with degree 89 found yet. In the second half of October, "missing pairs" were found:

Statistics for October, part 2:
...
Degree 88: 6
Degree 89: 3
Degree 90: 0
...

But that's not all! Two out of three pairs were present in one workunit! Moreover, each of the two workunits crunched by a computer of one participant! Consequently, we have 3 pairs, 2 workunits, 4 results and 3 participants:
whizbang from Ars Technica team.
killik from Czech National Team.
Administrator {11320}

Statistics for whole October:
Degree 81: 2651975
Degree 82: 645827
Degree 83: 142978
Degree 84: 27828
Degree 85: 4840
Degree 86: 718
Degree 87: 73
Degree 88: 12
Degree 89: 3
Degree 90: 1
Degree 91: 0
...
Degree 100: 0

Statistics for entire search:
Degree 81: 6539402
Degree 82: 1544999
Degree 83: 323992
Degree 84: 61825
Degree 85: 10094
Degree 86: 1618
Degree 87: 167
Degree 88: 28
Degree 89: 3
Degree 90: 1
Degree 91: 0
...
Degree 100: 0