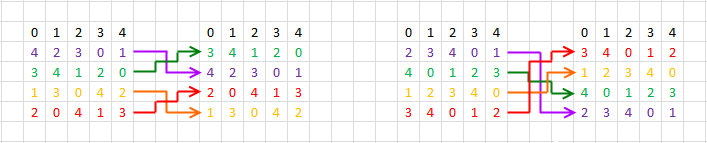
What is RakeSearch?
The enormous size of the diagonal Latin squares space makes it unfeasible to enumerate all its objects straightforwardly in reasonable time. So, in order to discover the structure of this space, sophisticated search methods are needed. In RakeSearch project, we implement an application that picks up separate pairs of mutually orthogonal DLSs, which allows to reconstruct full graphs of their orthogonality.
For account creation please use a Crunch_4Science invitation code. It is not needed when registering by BOINC Manager.
Already joined? Log in.
User of the Day
News
Processing of the square # 55 completed
Dear participants, processing of the square # 55 is fully completed! The square:
0 1 2 3 4 5 6 7 8 9 A B
1 2 0 4 7 8 9 3 A B 5 6
A 5 8 6 9 2 4 B 0 7 1 3
7 3 4 1 2 6 5 0 9 8 B A
5 8 A 9 B 0 7 6 1 3 2 4
6 9 B 8 A 7 0 5 3 1 4 2
8 A 5 B 6 1 3 9 2 4 0 7
B 6 9 5 8 4 2 A 7 0 3 1
9 B 6 A 5 3 1 8 4 2 7 0
4 7 3 0 1 B A 2 6 5 9 8
3 4 7 2 0 9 8 1 B A 6 5
2 0 1 7 3 A B 4 5 6 8 9
has 468362488 orthogonal mates which puts it on the 46th place of the rating which include now 6005 positions.
Thank you for project attention, support and donation of CPU time!
11 Jul 2025, 5:36:52 UTC
· Discuss
Processing of the square # 54 completed
Dear participants, processing of the square # 54 is fully completed! The square:
0 1 2 3 4 5 6 7 8 9 A B
1 2 3 4 5 0 B 6 7 8 9 A
3 4 5 0 1 2 9 A B 6 7 8
6 B A 9 8 7 4 3 2 1 0 5
A 9 8 7 6 B 0 5 4 3 2 1
7 6 B A 9 8 3 2 1 0 5 4
2 3 4 5 0 1 A B 6 7 8 9
8 7 6 B A 9 2 1 0 5 4 3
B A 9 8 7 6 5 4 3 2 1 0
9 8 7 6 B A 1 0 5 4 3 2
5 0 1 2 3 4 7 8 9 A B 6
4 5 0 1 2 3 8 9 A B 6 7
has 482707843 orthogonal mates which puts it on the 41th place of the rating which include now 5947 positions.
Thank you for project attention, support and donation of CPU time!
16 May 2025, 20:50:10 UTC
· Discuss
Processing of the square # 53 completed
Dear participants, processing of the square # 53 is fully completed! The square:
0 1 2 3 4 5 6 7 8 9 A B
1 2 0 4 5 3 8 6 7 B 9 A
3 4 5 0 1 2 9 A B 6 7 8
8 7 6 B A 9 2 1 0 5 4 3
7 6 8 A 9 B 0 2 1 3 5 4
B A 9 8 7 6 5 4 3 2 1 0
2 0 1 5 3 4 7 8 6 A B 9
9 B A 6 8 7 4 3 5 1 0 2
4 5 3 1 2 0 B 9 A 8 6 7
6 8 7 9 B A 1 0 2 4 3 5
5 3 4 2 0 1 A B 9 7 8 6
A 9 B 7 6 8 3 5 4 0 2 1
has 481458287 orthogonal mates which puts it on the 42th place of the rating which include now 5899 positions.
Thank you for project attention, support and donation of CPU time!
16 May 2025, 20:46:41 UTC
· Discuss
Processing of the square # 52 completed
Dear participants, processing of the square # 52 is fully completed! The square:
0 1 2 3 4 5 6 7 8 9 A B
1 2 3 4 8 9 A B 0 7 5 6
B 6 A 5 9 3 1 8 7 4 2 0
A 5 9 7 B 8 3 1 6 0 4 2
8 0 1 2 3 A B 9 4 5 6 7
6 A 5 9 7 4 2 0 B 8 3 1
9 7 B 6 A 1 8 3 5 2 0 4
2 3 4 8 0 7 5 6 1 B 9 A
7 B 6 A 5 2 0 4 9 3 1 8
5 9 7 B 6 0 4 2 A 1 8 3
4 8 0 1 2 6 7 5 3 A B 9
3 4 8 0 1 B 9 A 2 6 7 5
has 482008438 orthogonal mates which puts it on the 41th place of the rating which include now 5870 positions. Now "high part" of spectra of ODLS-12 looks like this (square # 52 marked by red):
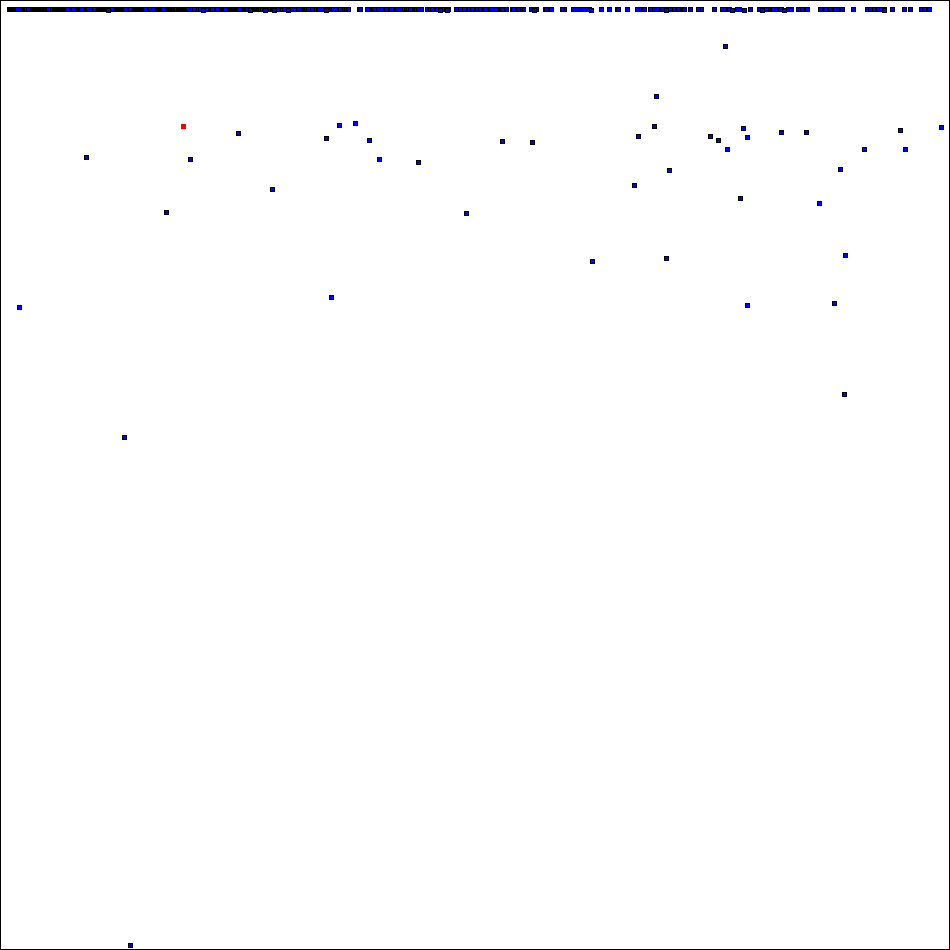
Thank you for project attention, support and donation of CPU time!
31 Dec 2024, 7:51:05 UTC
· Discuss
Processing of the square # 51 completed
Dear participants, processing of the square # 51 is fully completed! The square:
0 1 2 3 4 5 6 7 8 9 A B
1 2 0 4 7 6 A 3 B 8 5 9
5 6 A B 9 0 1 8 7 4 2 3
6 A 5 9 8 1 2 B 3 7 0 4
8 B 9 5 6 7 3 A 2 1 4 0
9 8 B A 5 4 7 6 1 0 3 2
7 3 4 0 1 8 B 2 A 6 9 5
4 7 3 2 0 9 8 1 6 5 B A
3 4 7 1 2 B 9 0 5 A 8 6
A 5 6 8 B 2 0 9 4 3 1 7
B 9 8 6 A 3 4 5 0 2 7 1
2 0 1 7 3 A 5 4 9 B 6 8
has 509396858 orthogonal mates which puts it on the 34th place of the rating which include now 5850 positions. Now "high part" of spectra of ODLS-12 looks like this (square # 51 marked by red):
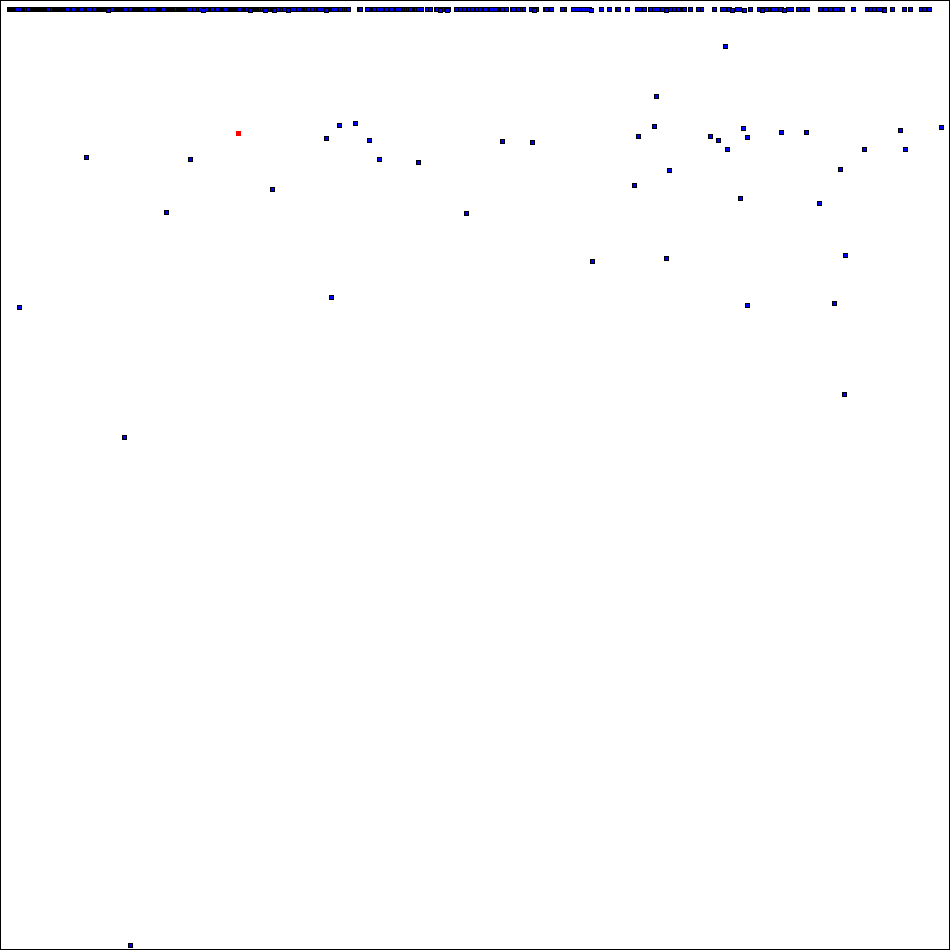
Thank you for project attention, support and donation of CPU time!
11 Dec 2024, 16:28:09 UTC
· Discuss
... more
News is available as an RSS feed

©2025 The searchers team, Karelian Research Center of the Russian Academy of Sciences

